子どもが未来を切り開いていく力を自分自身で身に付けていくことができるように,子どもの思いや願いを的確にとらえる必要がある。そのため,「成長課題の実現」,「基礎･基本の定着」,「学習の総合化」などの考え方を打ち出している。
『教える』から『創る』算数学習への転換→教師が子どもに『寄り添う』学習を
（教師が意図とする内容に近付けようとする支援だけでなく,子どもの考えや意見を十分に理解し,共に考え,問題解決にあたるという支援）
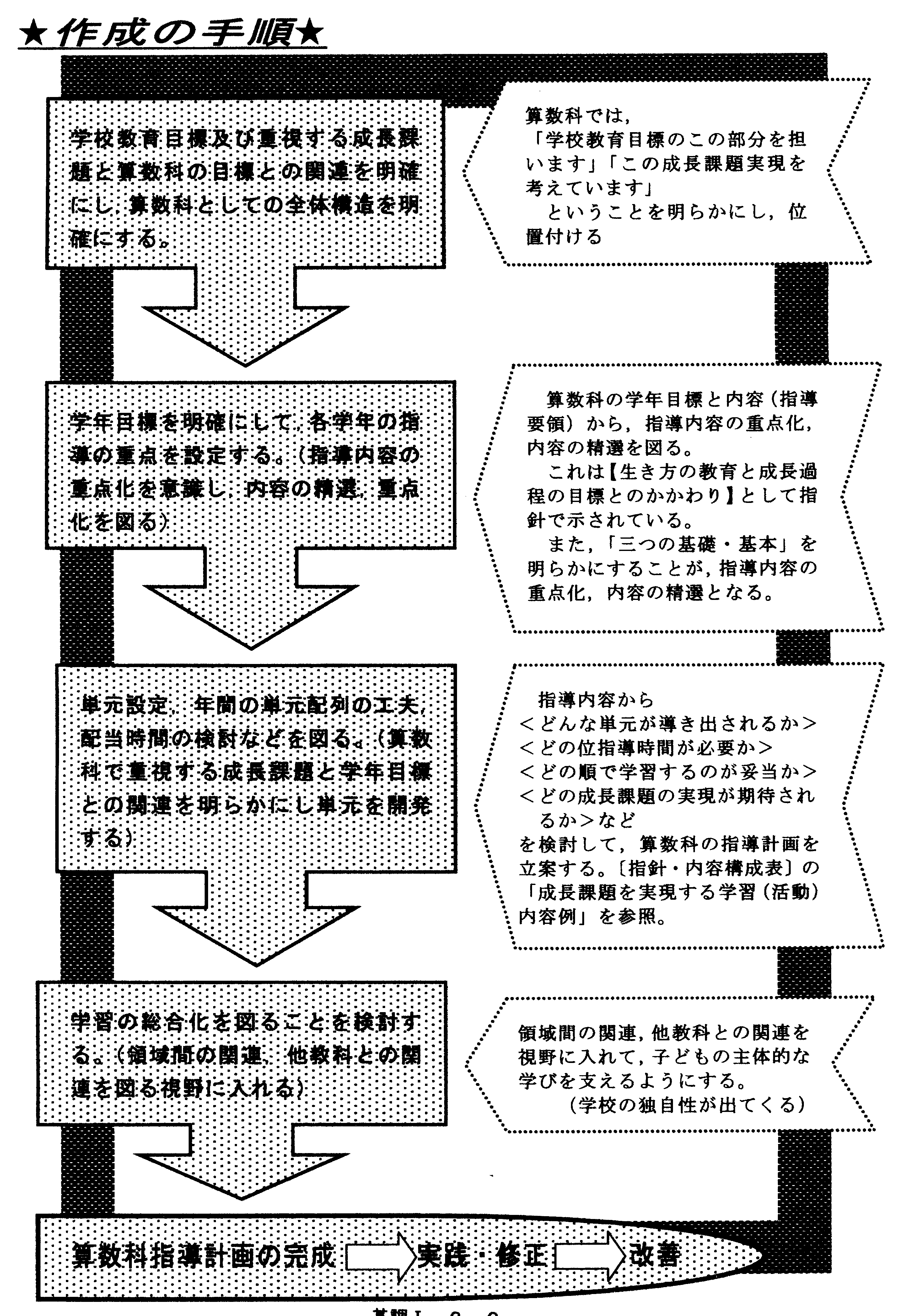
算数科年間指導計画の作成にあたっては
成長課題を把握し,それを位置付けること
基礎･基本の定着を図るために,指導内容との関連を明確にすること
内容相互の関連を図ること
子どもの興味･関心を大切にすること
を関連づけて取り組むことが大切
学校教育目標の具現化と算数科学習
16の成長課題(指針3p参照)を拠り所にして,学習集団におけるおおよその成長課題を把握し,その実現に向けた支援を明確にした年間指導計画を作成する
学校教育全体の中での算数科学習の果たす役割を明確にし,日常の事象に対して,子どもが興味･関心をもち,自ら課題を見付け,意欲的に問題解決を進めるといった創造性豊かな学習ができるよう,個に応じた指導や支援を工夫することを考えていく
A小学校の例
A小学校では,学校教育目標の設定に際して,学校の特色,子どもの実態,子ども,保護者･地域,そして教職員の思いや願いをもとに,学校教育目標に『自分らしさの発揮』を打ち出し,10の学習課題,23の成長課題から関連するものとして,
●10の学習課題から《共生･個性･生活》
●23の成長課題から《①⑤⑪⑭⑰⑳》
を設定。これらは,「横浜市小学校教育課程編成の指針算数科編」の算数科の16の成長課是をすべて網羅するものではない。学校教育目標を意識しながら年間指導計画を作成していくということ。
学習課題.成長課題の分析
A小学校では,10の学習課題から"共生･個性･生活"の三つを設定，それぞれについての分析してそれぞれが関連した年間指導計画の作成に取り組む。
例として「個性」について分析。問題解決の際に,自分の考えをもち,自分の考えに従い解決を進めることが不可欠である。その解決が,正しいものであっても,迂遠なものであっても,たとえ誤りであっても,そこには『自分の考え(=論理)』があるととらえる。このことがまさに,『自分らしさ(=個性)』である。この自分らしさを伸張するためには,問題解決の過程の練り上げの段階で,子ども同士のかかわりが重要である。そのため,練り上げの段階での子ども同士のかかわり方をより一層重視した年間指導計を作成していく。
実態の把握と成長課題
成長課題の実現に向けて,子どもの実態を把握し,年間指導計画に生かすこと。
学習環境の工夫
子ども一人ひとりが,安心して学習に取り組める学習環境作りの工夫。
① 学習集団の多様化(学級･学年の枠を超えた集団の編成,課題の違いによる小集団の編成など)
② 学習時間の弾力化(1単位時間の弾力化,モジュール方式の導入など)
③ 学習空間の多様化(教室内外の学校施設の利用,学習コーナーの設置など)
④ 「まち」とのネットワーク(学習の場を学校外に広げる,PC機器の利用や異校種間の交流の拡大･充実など)
学習課題の個性を具現化には子ども一人ひとりの特質を生かした学習の展開。
○ 式などの抽象的な表現が得意な子ども
○ 図を用いて図示することが得意な子ども
○ 言葉で自分の解決の過程を説明することが得意な子ども
成長課題を生かした算数科年間指導計画留意点
ア 子ども一人ひとりの成長課題を十分に把握した年間指導計画
･単元の時間配分や構成が,子どもの実態,興味･関心を十分に生かし,自ら問題意識をもち,主体的な問題解決ができる。
･問題解決にあたり見通しをもち,自分の考えで解決ができる。
･子どもの特徴を生かし,多様な考えを取り入れた問題解決に生かす。
･子どもの反応を十分に予想する。
イ 子ども一人ひとりの成長課題への適切な支援を考えた年間指導計画の作成
・自分らしさに気付いて学習を進めることができるよう,子ども一人ひとりの成長課題にそった支援を考える。
・自分の生活や既習内容をもとに自分らしさを伸ばすことができるよう,子ども一人ひとりが十分に自分の考えを出し切れる支援を考える。
･個に応じた教具や操作を生かす。
ウ 子ども一人ひとりの成長課題を生かし,子ども一人ひとりの学習の評価をし、以後の学習に生かす年間指導計画
・子ども一人ひとりに多様な個性に気付き,互いの個性を尊重し,評価し合い,学習を練り上げる。
・自分の考えを自らが評価し,互いに高め合いながら学習に生かしていく。
・学習のねらいを受けて,子どもの変容を評価し,以後の学習に生かす。
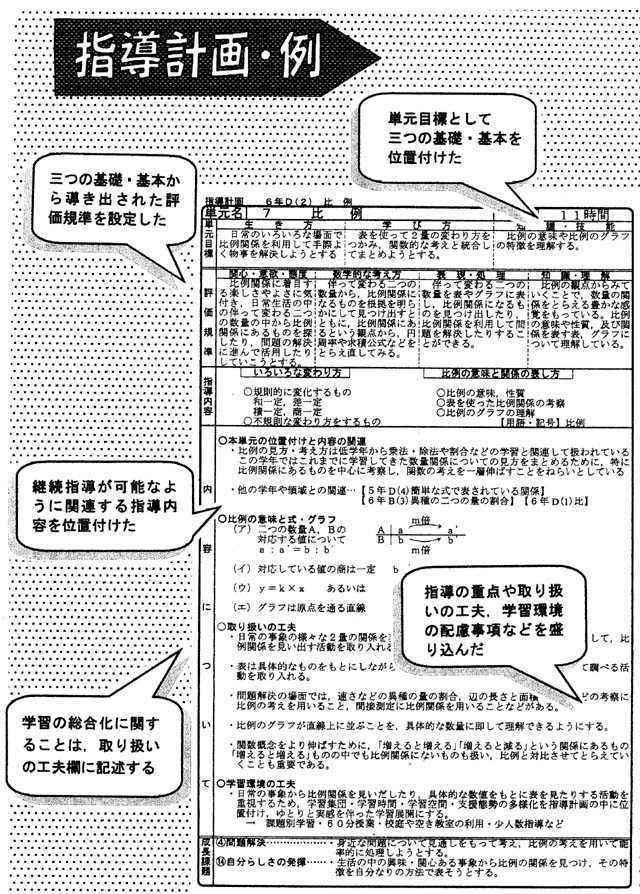
基礎・基本の定着を図るために指導内容との関連を明確にする
主体的に基礎･基本を身に付けていくために,内容構成表にある三つの基礎・基本を明確にとらえ,それらを確実に年間指導計画に位置付ける必要がある。
また,子どもが想起する課題や想定する数学的な考え方,解決方法などを可能な限り取り込んだ計画を作成するで,子どもに寄り添った支援が可能となる。
さらに,各学年の内容が,次の学年以降においても必要に応じて継続して指導できるように年間指導計画に位置付けておくことも大切である。
三つの基礎･基本と算数学習
生き方の基礎・基本
算数を生活に活用していこうとする生き方を生き方の基礎･基本。
「数理的な処理のよさを生活に生かすj「能率的に処理するよさを生活や物事の処理に生かす」「簡潔,明瞭,的確のよさを生活に生かす」など。
学び方の基礎･基本
既習事項や既存体験を基に数学的な見方や考え方を働かせて問題解決することや問題解決的な学習の方法を学び方の基礎･基本。
「一般化･理想化・関数の考えなどの数学的な考え方」「問題解決の方法としての,既習内容の活用,見積り･見通しなどの方針決定,振り返り」など。
知識･技能の基礎･基本
上記２つの基礎･基本を身に付けるために必要な知識や技能及び問題解決をする上で欠かせない知識や技能を知識・技能の基礎･基本。
「数の仕組みや概念」「演算決定の根拠や計算方法」「量の概念や測定の方法」「図形の見方一性質と作図方法」「数量関係のとらえと表示の方法」など。
「生き方の教育」の推進において算数科が担う面は
ア 算数の内容面で学習したことを用いて日常生活の諸問題の解決に生かすこと
イ 問題解決の方法や方略を生活の諸問題の解決に生かそうとすること
ウ 数学的な考え方を他の問題解決の場の解決に生かそうとすること
年間指導計画に子どもの思いや願い,実態をもとに,学校としてどこに重点そおき,どのような学習を組み立てていくか明確にしていく必要がある。
内容相互の関連を図る
子どもが日常事象の中で様々な数理的な事象の関係をとらえ,問題解決していくことができるよう,内容の相互関連や他の教科との関連を図る。学習の総合化と合わせて考えてみる。
(1) 学習の総合化に向けて
ア 子どもの経験や興味関心,既習事項が生かされ,主体的･自発的な学習であること
イ 日常事象に関連付けて,より一層間通解決が図れる学習であること
ウ 子ども自身がもつ課題の解決が新たな課題の発見や解決につながる学習であること
エ 総合的な算数的活動を通して,問題の解決にあたるような学習であること
(2) 学習の総合化を図った学習活動
ア 算数科の中で学習の総合化を図る学習活動
（A）単元を超え,内容の相互を関連付けた学習活動･領域や内容の枠組を超えて課題追究に必要な内容の視点からとらえ直し,単元構成をする。
(B)学年を超え,内容の相互を関連付けた学習活動
上学年以降だけでなく,下学年での学習内容を新しい視点でとらえ直し,単元構成をする。
イ 各教科等との関連で学習の総合化を図る学習活動
子どもの主体的な学びが,内容的･方法的に他の教科等と密接なかかわりをもち,関連付けて扱う方が効果的であると思われる場合に,他教科等との関連を考えて単元構成する。
ウ各教科,道徳,特別活動という枠組にとらわれないで学習の総合化を図る
子どもの学びが,算数科を超えて広がっていく場合,教科の枠組にとらわれず問題解決を図る。
学習の総合化を考えるとき,子ども一人ひとりの成長課題と関連させて,算数科の内容の特質としての系統性を生かした単元配列の工夫や,他教科との関連も考えた単元配列の工夫をする。
→「学級における年間指導計画一覧表」などの作成が有効になる。
→学校で身に付けた算数の知恵を生活の場にも応用し,活用していくような働きかけや学習の場を工夫していくこともこれからの教育活動には大切なこととなる。
子どもの興味・関心を大切にする
数理的な学習の推進
算数的活動を通して,幅広い数学的なものの見方や考え方が身に付くような学習場面。
子どもの興味･関心を生かしながら,数理的な学習を推進するためには
①目的に応じて作業的,体験的な活動を取り入れた学習を構成し,活動の楽しさを味わいながら数理的な処理のよさに気付き,学ぶことの大切さを味わうこと
②子どもの思考の流れや生活のリズム等に配慮し,ゆとりをもって学習が進められるようにすること
③学習をとおして,互いにふれあい,学び合い,高め合う学習集団を設定することなど。
体験する算数学習
教室内だけの学習ではなく,廊下や体育館･校庭などの学校の施設全体や学校の外に学習の場を設けていく。自分の体を使い,動かして体験したり,確かめたりする算数学習や多くの人と一緒に考えていく学習の工夫について考える。
